
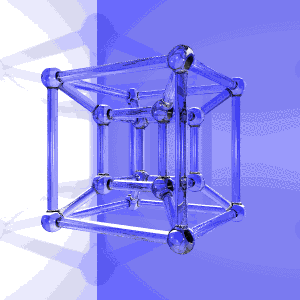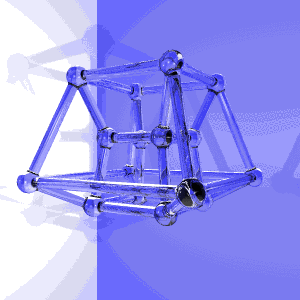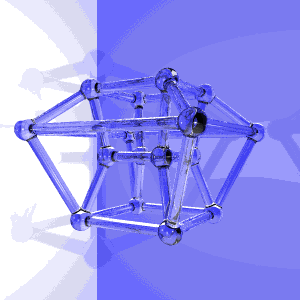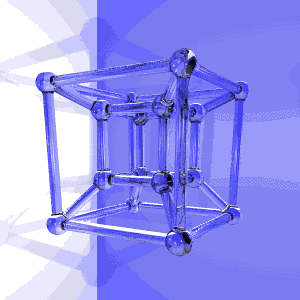
The pixels colored with different shades of blue are forward-facing faces, and the black pixels are backward-facing faces.Īs you can see, the 3D model becomes non-convex from time to time, as it looks like a face or two are "forgotten" and we can see the "inside", back-facing faces behind. The resulting intersections, being 3D objects, are directly displayed on the screen with no further transformation. The hypercube is decomposed in 4D tetrahedras, which are subsequently intersected with a 3D hyperplane, which is defined by the position of the camera and the direction of its (3D) viewing frustum. the hypercube (tesseract) is a 4th dimensional shape, and therefore all you are seeing is what we imagine it should. The principle of the visualisation is a simple application of the aforementioned algorithm. The problem resides in this visualisation of a unit hypercube rotating around its center on the XZ and ZW canonical planes by equal angles, in that order (WebM video) :

Then, for each edge that intersects the hyperplane (ie edges for which the two vertices lie in opposite half-spaces), add to the array the intersection between that edge and the hyperplaneĪlthough I have not written a rigorous proof for this, I find empirically that you only get points, lines, triangles, quadrilaterals or tetrahedras out of this algorithm (or at least, I have never encountered a counter-example).In fact, even a square is just a 2-dimensional extension of a line segment, which is itself a 1-dimensional extension of a point. If at least one point is inside the hyperplane, then add to the array all the vertices that are inside the hyperplane. A hypercube (or tesseract) is the 4-dimensional extension of a cube in the same way that a cube is the 3-dimensional extension of a square.If all points are in the same half-space, terminate with an empty intersection.Determine which of the tetrahedron's points lie in opposite half-spaces.My algorithm fills an array with vertices, and builds the resulting intersection as being the convex polygon or polyhedron uniquely defined by said vertices, on the basis that the intersection of a convex set with a hyperplane is also convex. Because of my lack of visualization (obviously), and for computer rendering purposes, I am using a computational approach. I am trying to compute all possible intersections between a tetrahedron lying in 4D space and a non-centered 3D hyperplane.


 0 kommentar(er)
0 kommentar(er)
